This is a simple KNN implementation for supervised learning. It deals with examples with known classes. You can find K-means clustering implementation in my next post to come.

Dummy dataset

First let’s make some dummy data with training examples and labels and test examples some approximate labels. I chose 2 classes based on x and y coordinates (one is more on the positive side, the other – negative).

X_train = [
    [1, 1],
    [1, 2],
    [2, 4],
    [3, 5],
    [1, 0],
    [0, 0],
    [1, -2],
    [-1, 0],
    [-1, -2],
    [-2, -2]
]

y_train = [1, 1, 1, 1, 1, 2, 2, 2, 2, 2]

X_test = [
    [5, 5],
    [0, -1],
    [-5, -5]
]

y_test = [1, 2, 2]

KNN theory

Right,  supervised KNN works by finding the numerically “closest” neighbors and seeing what those neighbors classes are like. Then taking the one that’s more popular among the n neighbors and saying that’s most probably the class for the data point you’re asking about.

One of the ways to calculate the “distance” is to do just that – calculate the distance with Euclidean distance from geometry. The formula looks like this for two points with two parameters A(a1, a2) and B(b1, b2) :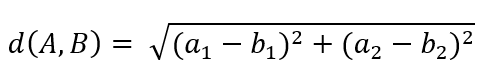

It can work with many more features not just two, you just keep summing the corresponding squared subtractions one after the other.

Euclidean distance in code

In code it would look like this:

import math

def euclidean_dist(A, B):
    return math.sqrt(sum([(A[i]-B[i])**2 for i, _ in enumerate(A)]) )

The function euclidean_dist takes as input two points regardless of how many features they have and outputs the Euclidean distance.

KNN in code

Now we just have to find the distance from each test set element to all of the training set elements and get the most popular class in the n closest neighbor classes.  Here function knn does that.

def knn(X_train, y_train, X_test, k=1):
    y_test = []
    for test_row in X_test:
        eucl_dist = [euclidean_dist(train_row, test_row) for train_row in X_train]
        sorted_eucl_dist = sorted(eucl_dist)
        closest_knn = [eucl_dist.index(sorted_eucl_dist[i]) for i in xrange(0, k)] if k > 1 else [eucl_dist.index(min(eucl_dist))]
        closest_labels_knn = [y_train[x] for x in closest_knn]
        y_test.append(get_most_common_item(closest_labels_knn))
    return y_test

Finally, we need a helper function to find the most popular item in an array. I chose a solution where I put the class as a key in a dictionary and keep increasing the value for the key to count occurrences:

from collections import defaultdict
from operator import itemgetter

def get_most_common_item(array):
    count_dict = defaultdict(int)
    for key in array:
        count_dict[key] += 1
    key, count = max(count_dict.iteritems(), key=itemgetter(1))
    return key

Now we can test this out with our custom dataset setting neighbor count to 2:

print knn(X_train, y_train, X_test, k=2)  # output: [1, 1, 2]

And we can see that this somewhat matched my imagined labels [1, 2, 2].

You can find the whole core on my Github repository or here below: