Category Archives: ML

ML, python

Simple KNN implementation in Python 2.7

Leave a comment

This is a simple KNN implementation for supervised learning. It deals with examples with known classes. You can find K-means clustering implementation in my next post to come.

Dummy dataset

First let’s make some dummy data with training examples and labels and test examples some approximate labels. I chose 2 classes based on x and y coordinates (one is more on the positive side, the other – negative).

X_train = [
    [1, 1],
    [1, 2],
    [2, 4],
    [3, 5],
    [1, 0],
    [0, 0],
    [1, -2],
    [-1, 0],
    [-1, -2],
    [-2, -2]
]

y_train = [1, 1, 1, 1, 1, 2, 2, 2, 2, 2]

X_test = [
    [5, 5],
    [0, -1],
    [-5, -5]
]

y_test = [1, 2, 2]

KNN theory

Right,  supervised KNN works by finding the numerically “closest” neighbors and seeing what those neighbors classes are like. Then taking the one that’s more popular among the n neighbors and saying that’s most probably the class for the data point you’re asking about.

One of the ways to calculate the “distance” is to do just that – calculate the distance with Euclidean distance from geometry. The formula looks like this for two points with two parameters A(a1, a2) and B(b1, b2) :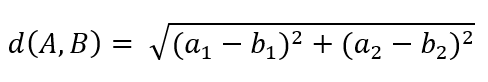

It can work with many more features not just two, you just keep summing the corresponding squared subtractions one after the other.

Euclidean distance in code

In code it would look like this:

import math

def euclidean_dist(A, B):
    return math.sqrt(sum([(A[i]-B[i])**2 for i, _ in enumerate(A)]) )

The function euclidean_dist takes as input two points regardless of how many features they have and outputs the Euclidean distance.

KNN in code

Now we just have to find the distance from each test set element to all of the training set elements and get the most popular class in the n closest neighbor classes.  Here function knn does that.

def knn(X_train, y_train, X_test, k=1):
    y_test = []
    for test_row in X_test:
        eucl_dist = [euclidean_dist(train_row, test_row) for train_row in X_train]
        sorted_eucl_dist = sorted(eucl_dist)
        closest_knn = [eucl_dist.index(sorted_eucl_dist[i]) for i in xrange(0, k)] if k > 1 else [eucl_dist.index(min(eucl_dist))]
        closest_labels_knn = [y_train[x] for x in closest_knn]
        y_test.append(get_most_common_item(closest_labels_knn))
    return y_test

Finally, we need a helper function to find the most popular item in an array. I chose a solution where I put the class as a key in a dictionary and keep increasing the value for the key to count occurrences:

from collections import defaultdict
from operator import itemgetter

def get_most_common_item(array):
    count_dict = defaultdict(int)
    for key in array:
        count_dict[key] += 1
    key, count = max(count_dict.iteritems(), key=itemgetter(1))
    return key

Now we can test this out with our custom dataset setting neighbor count to 2:

print knn(X_train, y_train, X_test, k=2)  # output: [1, 1, 2]

And we can see that this somewhat matched my imagined labels [1, 2, 2].

You can find the whole core on my Github repository or here below:

ML, NLP, python, text processing

Cleaning Text for Natural Language Processing Tasks in Machine Learning in Python

Leave a comment

Often when I work with text I need it to be clean. That is to remove gibberish or symbols/words I don’t need and to make all letters lowercase.

For example, a “dirty” line of text:

text = ['This is dirty TEXT: A phone number +001234561234, moNey 3.333, some date like 09.08.2016 and weird Čárákterš.']

Using Python2.7:

1) Read the line from list:

for line in text:
    # do something with line

or read from file:

with open('file.txt', 'r') as f:
    for line in f:
        # do something with line

2) Decode the line to utf8 from a string of bytes to work with special symbols:

line = line.decode('utf8')

3) Remove the symbols you don’t need. With replace() you can stack as many replace operations as you want.

line = line.replace('+', ' ').replace('.', ' ').replace(',', ' ').replace(':', ' ')

4) Remove numbers. Here you can use regex \d+. Because dots have already been removed we only need to check for whole numbers.

line = re.sub("(^|\W)\d+($|\W)", " ", line)

This regex matches the start of line ^ or whitespace, digits, end of line $ or whitespace to a space.

Alternatively you can just check if a word evaluates to a number by a simple function – is_digit() attempts to turn a string into int. If it succeeds, then the function returns true.

def is_digit(word):
    try:
        int(word)
        return True
    except ValueError:
        return False

Use this function on each word in the line by splitting the line on space with line.split(). New line array will hold only those words that are not numbers. At the end the array is joined together to a string.

new_line = []
for word in line.split():
    if not is_digit(word):
        new_line.append()
line = " ".join(new_line)

5) Now only lowercase and special characters remain. As lowercase only supports Latin letters, the special characters need to be turned to Latin. This can be done using Transliterate Python package or by hand. Here is a simple transliteration dictionary made from lists of character pairs:

cedilla2latin = [[u'Á', u'A'], [u'á', u'a'], [u'Č', u'C'], [u'č', u'c'], [u'Š', u'S'], [u'š', u's']]
tr = dict([(a[0], a[1]) for (a) in cedilla2latin])

In this way you can have multiple simbols to stand for one special symbol (like German [u’ä’, u’ae’]).
With the dictionary I can recreate letters in Latin:

def transliterate(line):
    new_line = ""
        for letter in line:
            if letter in tr:
                new_line += tr[letter]
            else:
                new_line += letter
    return new_line

And call the transliterate function:

line = transliterate(line)

6) After clearing away unnecessary symbols, finally I can lowercase the line:

line = line.lower()

And finally the line is reduced to simple Latin characters.

print line
>> this is dirty text a phone number money some date like and weird carakters

If you need to retain some numbers or check for other fields then go ahead and write more specific regexes.  However, regexes in Python use backtracking that makes them n-squared in terms of speed. This can slow you down especially if you are working with millions of lines.

As a side note a more general cleaning method that leaves only Latin characters can be to check for the ASCII value of each letter with ord().

def get_latin(line):
    return ' '.join(''.join([i if ord(i) >=65 and ord(i) <=90 or  ord(i) >= 97 and ord(i) <= 122 else ' ' for i in line]).split())

Full code of the above description is available below or here: